Hey guys! Welcome back to a new blog on Data structure and Algorithms. If you do not know then I tell you that I have a complete DSA series on my blog where you can read blogs related to DSA topics.
In this blog, we will be talking about Stacks and queues in detail because this topic is so easy and asks quite a lot in interviews and that is why you cannot miss this. So let's start with the definitions.
What is a Stack?
Stack basically is a linear data structure that serves as a collection of elements. You must be very familiar with this term in computer memory. Stack memory is widely used in alot of operations and recursion is based on stack memory only.
Stack data structure serves two main operations push, and pop. Push means adding the item and pop means removing the item.
Now let's go in-depth about this.
Think about stack as a plate pack, whenever you go to a wedding you see plates on the table. The order in which the plates are arranged just one on the other, stacked is all about that.

Now if someone wants a plate he/she will take the uppermost plate and this same happens with the stack memory.
Stack follows the LIFO principle which is Last in first out means the element inserted at last will be the first element to come out from the list.
Now you must have built an understanding of what stacks are all about.
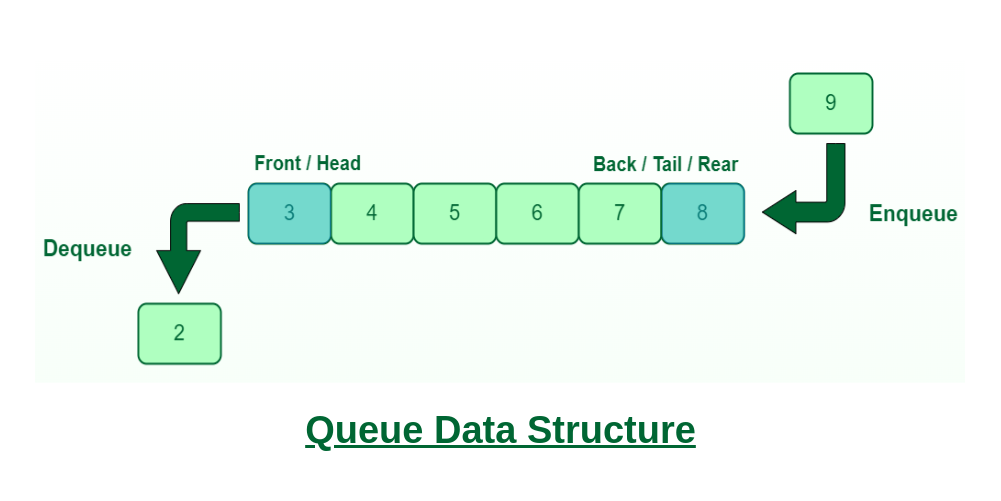
What is a Queue?
The queue data structure as the name suggests works as a queue. Hence it follows the FIFO principle. It means the element inserted first will be the first to come out from it.
Difference between Stack and Queue data structures
| Stacks | Queues |
| Insertion and deletion in stacks take place only from one end of the list called the top. | Insertion and deletion in queues take place from the opposite ends of the list. Insertion happens from the back and deletion happens from the front. |
| Insert operation is called push operation. | Insert operation is called enqueue operation. |
| Delete operation is called pop operation. | Delete operation is called dequeue operation. |
| In stacks, we maintain only one pointer to access the list, called the top, which always points to the last element present in the list. | In queues, we maintain two pointers to access the list. The front pointer always points to the first element inserted in the list and is still present, and the other pointer always points to the last element. |
| Stack is used in solving problems and works on recursion. | The queue is used in solving problems having sequential processing. |
| Stack does not have any types. | The queue is of three types – 1. Circular Queue 2. Priority queue 3. double-ended queue. |
Implementation of Stack
If we build our own stack then there are some aspects that we need to consider. Internally stack is just an array having some properties.
public class customStack { // Class name
protected int[] data; // An Array
private static final int DEFAULT_SIZE = 10; // Its default size
int ptr = -1; // Making a pointer that will be help in iteration
public customStack(int size) { // Constructor
this.data = new int[size];
}
public customStack() {
this(DEFAULT_SIZE);
}
Push Function
To push the element first we need to check if the array is full or not. If it is full then we cannot add any new elements.
Otherwise, we just increase the pointer by one and place the item at the given index.
public boolean push(int item){
if (isFull()){
System.out.println("It is full");
return false;
}
ptr++;
data[ptr] = item;
return true;
}
private boolean isFull() {
return ptr == data.length-1; // Ptr is at last index
}
Pop Function
To pop the element we need to check if the stack is empty or not, if it is empty then we will throw an expectation that we cannot delete from an empty stack.
Otherwise, just identify the last inserted element and decrease the pointer by 1.
public int pop() throws Exception {
if (isEmpty()){
throw new Exception("Cannot fill");
}
int removed = data[ptr];
ptr--;
return removed;
}
private boolean isEmpty(){
return ptr == -1;
}
Peek Element of the Stack
The peek element is the last element inserted at the stack so when we look at the stack from the top we will see the last element and that is called the peek element.
private int peek() throws Exception {
if (isEmpty()){
throw new Exception("Cannot see");
}
return data[ptr];
}
private boolean isEmpty(){
return ptr == -1;
}
Implementation of Queue
The internal implementation of the queue is quite similar to the stack we just need a few more logic to achieve the functionality.
public class customQueue {
private final int[] data;
private static final int DEFAULT_SIZE = 10;
int end = 0; // jUst working as a size
public customQueue() {
this(DEFAULT_SIZE);
}
public customQueue(int size) {
this.data = new int[size];
}
Insert Function
public void insert(int item){
if (isFull()){
return;
}
data[end] = item;
end++;
}
public boolean isFull(){
return end == data.length;
}
Remove Function
While removing, the element inserted at first will be the first one to be removed. Hence will be removing the first element of the array and then increasing its length by 1.
public int remove() throws Exception{
if (isEmpty()){
throw new Exception("It is empty");
}
int removed = data[0];
for (int i = 1; i <end; i++) {
data[i-1] = data[i];
}
end--;
return removed;
}
public boolean isEmpty(){
return end == 0;
}
Display Function
To display all the elements we need a function also.
public void display(){
for (int i = 0; i <data.length; i++) {
System.out.print(data[i] + " ");
}
}
Inbuilt Queue Object
To an object of an inbuilt queue class, we need to write
Queue<Integer> queue2 = new LinkedList<>(); // Queue is just type of linkedlist
queue2.add(34);
queue2.add(54);
queue2.add(76);
System.out.println(queue2);
Thank You 🙏
Hope you like this article and the few you do, you can sponsor this blog or can buy me a coffee. Thank you, and see you in the next blog.


