What is Backtracking Algorithm? | How to Solve Maze Problems? Data Structure & Algorithms
Hey Dear, Welcome again to my blog, other folks like you have enrolled in my daily newsletter and I think you should not miss that. So please subscribe to my Newsletter for daily technical blogs.
Today we will be covering a very important topic for interviews, Backtracking. A lot of people have written blogs on this but trust me you are a lucky one who found this blog because it is the best one.
My motive is that you shouldn't be having any doubts related to Backtracking after this blog. If you are preparing for FAANG (MAANG) you cannot miss this. So let's start the blog now.
What are the Prerequicts for Backtracking?
The prerequisites for backtracking are -
Subset Problems practice ✅
String Questions ✅
Recursion in Arrays ✅
Permutations and Combination Recursion ✅
What are Maze Problems?
Suppose you are having a 3*3 Matrix. If you are at (0,0) and you wanna go to (2,2) then what are all the possible paths you can figure out? These problems are where you need to find paths, and reach a particular destination these problems are called Maze Problems.
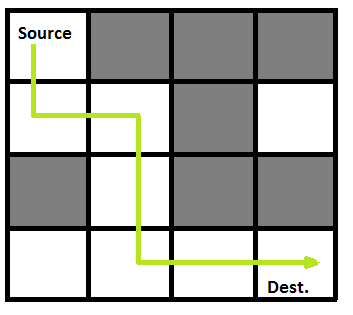
In maze problems, you generally have given the approaches to go with. Like in the above example to reach 3*3 you can follow two approaches to go Down or Right.
Question: What can be the possible paths you can follow to reach (2,2) in a 3 by 3 matrix?
Answer: RRDD, DDRR, RDDR, DRDR, and DRRD. These are all the possible paths you can take. Now let's think about how to build a recursion out of it.
Intuition Behind Maze-Problems
If you notice that if you are at any last column like (0,0) or (1,2) you have only one path. For example, if you are at (0,2) you can go only downwards. If you are at (2,0) you can go only toward the right.
Now in recursion, you break bigger problems into smaller ones. So what is the bigger problem for recursion? The bigger problem is to get all the paths that reach the last column of the last row.
Now ask yourself what ways you can go with it. The answer is Two✅. One toward the right➡ and one toward the down⬇. So how many recursive calls will be needed? Two.
Approach
Now let me show you a recursive tree. You are at (0,0) and you have to reach (2,2)
(0,0)⬇(1,0)➡(0,1) || (1,0)⬇(2,0)➡(1,1) || (2,0)⬇(base condition - return)➡(2,1) || (2,1)⬇(base condition - return)➡(2,2) || Answer DDRR✅
This is the tree of one of the paths. You start from (0,0) and you make two calls one for the right and one for the down and then so on.
Code
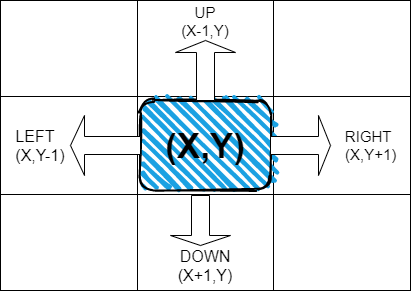
Now let's see the implementation of the Approach. Tell me how many variables in the argument we need. So the answer will be 3, why? So one is the number of rows, the second, is the number of columns, and then the String to store the Path.
public static void mazePath(int row, int col, String path){
// Base condition
if (row==2 && col==2){
System.out.println(path);
return;
}
// At the last row or col we need to prevent it to exceed the matrix.
if (row>2 || col >2){
return;
}
// For right call we increase the col
mazePath(row,col+1,path+"R");
// For down call we increase the row
mazePath(row+1,col,path+"D");
}
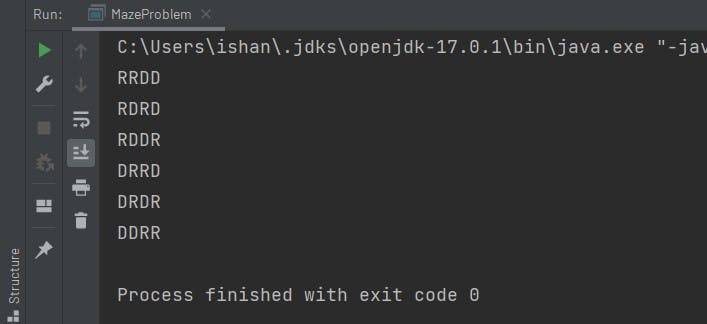
These are all the paths that are needed. Now your homework is -
You need to return that how many paths can be there two reach the destination. And comment your code below with your answer and I will give you the shoutout.
Maze With Diagonal
Now tell me how difficult it would be if I give you one more direction. Suppose Diagonal also. What will you do? It's simple just make one more recursive call in which both row and column will be increasing by 1 that is it.
Now you will ask why I am increasing both row and column then Diagonal always comes when row and column are equal.
Note: There will be one extra condition. When do we want the diagonal call to run? Only when Row and Col are equal.
// Maze Path Problem With Diagonal In list
public static ArrayList<String> mazePathDiagonal(int row, int col, String path){
// Base condition
if (row==2 && col==2){
ArrayList<String> ans = new ArrayList<>();
ans.add(path);
return ans;
}
// At the last row or col we need to prevent it to exceed the matrix.
ArrayList<String> ans = new ArrayList<>();
if (row<2){
// For down call we increase the row
ans.addAll(mazePathDiagonal(row+1,col,path+"V"));
}
if (col<2){
// For right call we increase the col
ans.addAll(mazePathDiagonal(row,col+1,path+"H"));
}
// For Diagonal, we increase both row and col
if (row==col){ // Only when row and col is equal and not exceeding the matrix
ans.addAll(mazePathDiagonal(row+1,col+1,path+"D"));
}
return ans;
}

You just need to add a simple condition so that you can be able to call diagonal only when row and col are equal.
Maze With Obstacles
This is one of the most popular sets of problems that comes in Maze. What is it? Let's see.
In this particular set of problems, there will be a column where you cannot go.
Suppose, At x and y there is a river. Now the task is you have to give all the possible paths excluding this particular column
Approach
Tell me, in a 3 by 3 matrix where is the river? It's at (1,1). So to stop our code from going there we just need to add One condition. Think about it and Look at the code later
Code
// Maze Path Problem Obstacles
public static void mazeWithObstacles(int row, int col, String path){
// Base condition
if (row==2 && col==2){
System.out.println(path);
return;
}
// At the last row or col we need to prevent it to exceed the matrix.
if (row>2 || col >2){
return;
}
if (row==1 && col==1){
return;
}
// For right call we increase the col
mazeWithObstacles(row,col+1,path+"R");
// For down call we increase the row
mazeWithObstacles(row+1,col,path+"D");
}
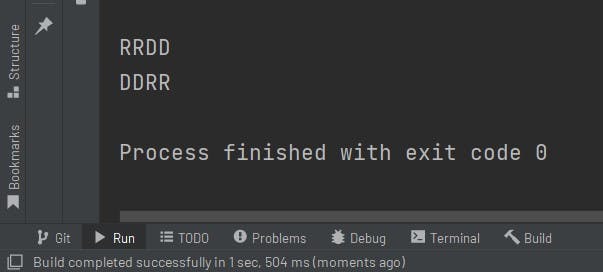
Hope you understood the code and what we are doing with how we are doing it.
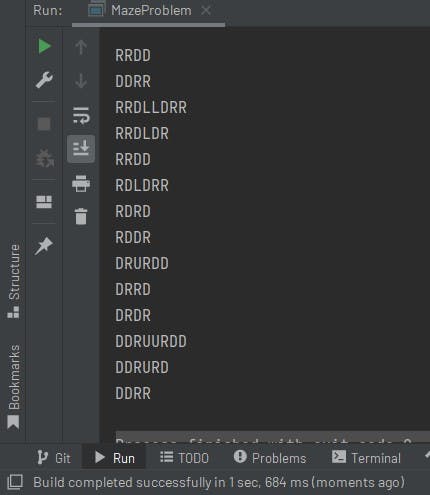
Maze All Path
Now here comes the real backtracking problem. In this problem, you are having all the directions (up, right, left, down). If you will try the above approach in this question you will get an error which is stack overflow.
Now you will ask why?

So the answer will be, You are adding four recursive calls. That will cause the recursion to come to where it all begins. And recursive calls will start running in the loop and it will be stuck in that.
That is why we need to track the movement of our recursive calls and that is what backtracking is all about.
What is BackTracking?
The changes that a recursive call makes should not be available for consideration again and when the recursion stack starts getting empty the calls start to undo all those changes making that path available again for further calls. This process is called Backtracking.
All that I said just now will go over your head if you will not try this on pen and paper. So kick out your laziness.

Approach
Now think that you are having a maze
0 1 2
0{true,true,true}
1{true,true,true}
2{true,true,true}
➡ if you start from 0,0 and takes a path of down you will mark 0,0 as false because you have visited that path. So it will become
0 1 2
0{False,true,true}
1{true,true,true}
2{true,true,true}
0 1 2
0{False,true,true}
1{Flase,true,true}
2{true,true,true}
➡ Just like this you will complete a whole path and after one path you will mark very coloumn as true again and print the path.
By this you will save the recursive calls from looping around.
Code
// Maze Path All path
public static void mazeWithAllPath(int row, int col, String path, boolean[][] maze){
// Base condition
if (row==maze.length-1 && col==maze[0].length-1){
System.out.println(path);
return;
}
if (!maze[row][col]){
return;
}
maze[row][col] = false; // Making the path false as we make calls
// Up
if (row>0){
mazeWithAllPath(row-1,col,path+"U",maze);
}
// Left
if (col>0){
mazeWithAllPath(row,col-1,path+"L",maze);
}
// For right call we increase the col
if (col<maze[0].length-1){ // the last coloumn
mazeWithAllPath(row,col+1,path+"R",maze);
}
// For down call we increase the row
if (row<maze.length-1){ // The last row
mazeWithAllPath(row+1,col,path+"D",maze);
}
maze[row][col] = true; // Undo all the changes for reuse
}
Thank You

If you found this blog helpful please do Like and comment. I always try to deliver the best I can. If you have any doubts feel free to ask and I will be resolving that for sure.

