Table of contents
Hey guys! Welcome to the new article on Data Structure. Today we will be talking about a very interesting data structure called Heap. Do not confuse Heap and priority Queue as it is the same thing, Why? I will be clearing it up in this article stay tuned.
What is Heap?
So to be very precise Heap is a Binary Tree stored Linearly and satisfies the conditions of CBT(Complete Binary Tree) and Priority. Now, what is that mean? Let's see.
One more thing the prerequisites for this is to know generics, Comparator, and Comparable.
First of all resolve this confusion that a bunch of students have. Is heap data structure is same as Heap memory? No, Heap memory has nothing to do with the heap data structure.
Heap is a special Binary Tree that satisfies the two conditions -
Complete Binary Tree - This means every node will have two child nodes and it will be filled in left to right manner.
Priority Queue - This means the client will get an element depending on the element's priority. Let's understand it in depth
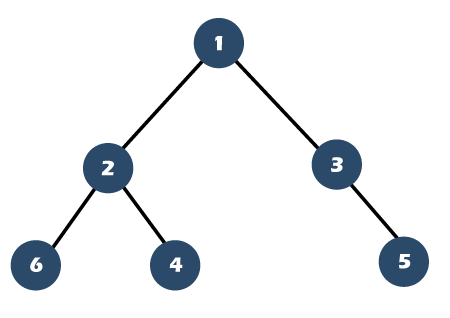
Priority Queue
A priority queue is represented as a balanced binary heap: the two children of the queue[n] are queue[2(n+1)] for left and queue[2(n+2)] for right.
This is the way we use Priority Queue. If you see elements were added in an unsorted manner and we are just adding and removing.
Now the question is why it is stored in an unstored manner when it is a priority queue and if it is stored in an unsorted manner then why does removing give us an element in a sorted manner? Let's resolve these doubts.
As I mentioned Priority Queue is a heap and the heap is a binary tree so the priority queue is stored as a binary tree. And when we remove the elements it gives you elements while satisfying the condition of priority. Call it heap or priority queue, it is the same thing.
Now let's understand another simple thing. Heaps are of two types -
- Min-Heap - The parent node will be smaller than the child nodes.
- Max - Heap - The child node will be smaller than the parent node.
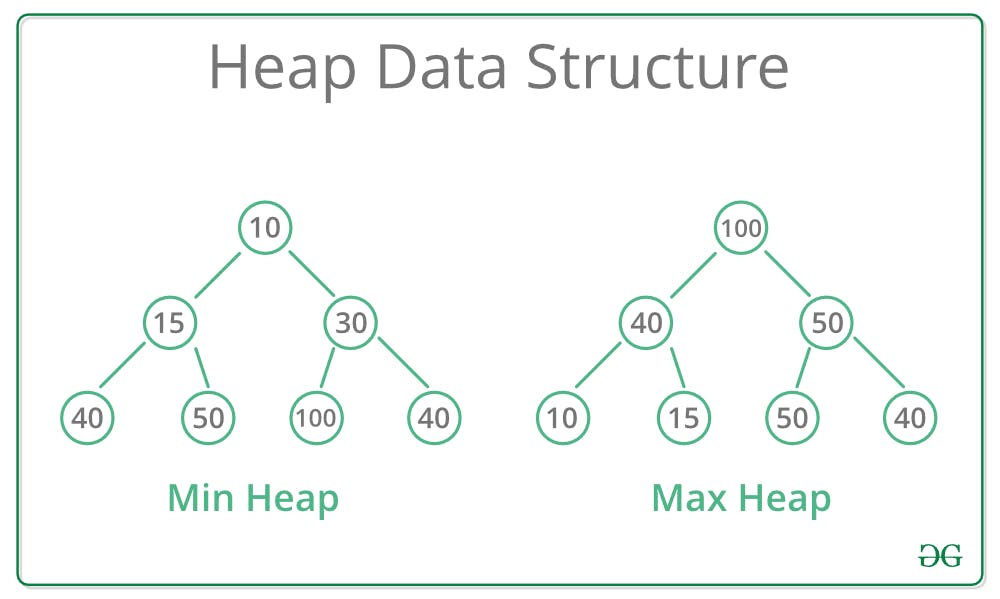
Heap Implementation
To make a custom Priority Queue or Heap we need to add a few functionalities to it such as -
- Size
- Is Empty
- Add
- Remove
- Display
- Peek
Let's try to build it.
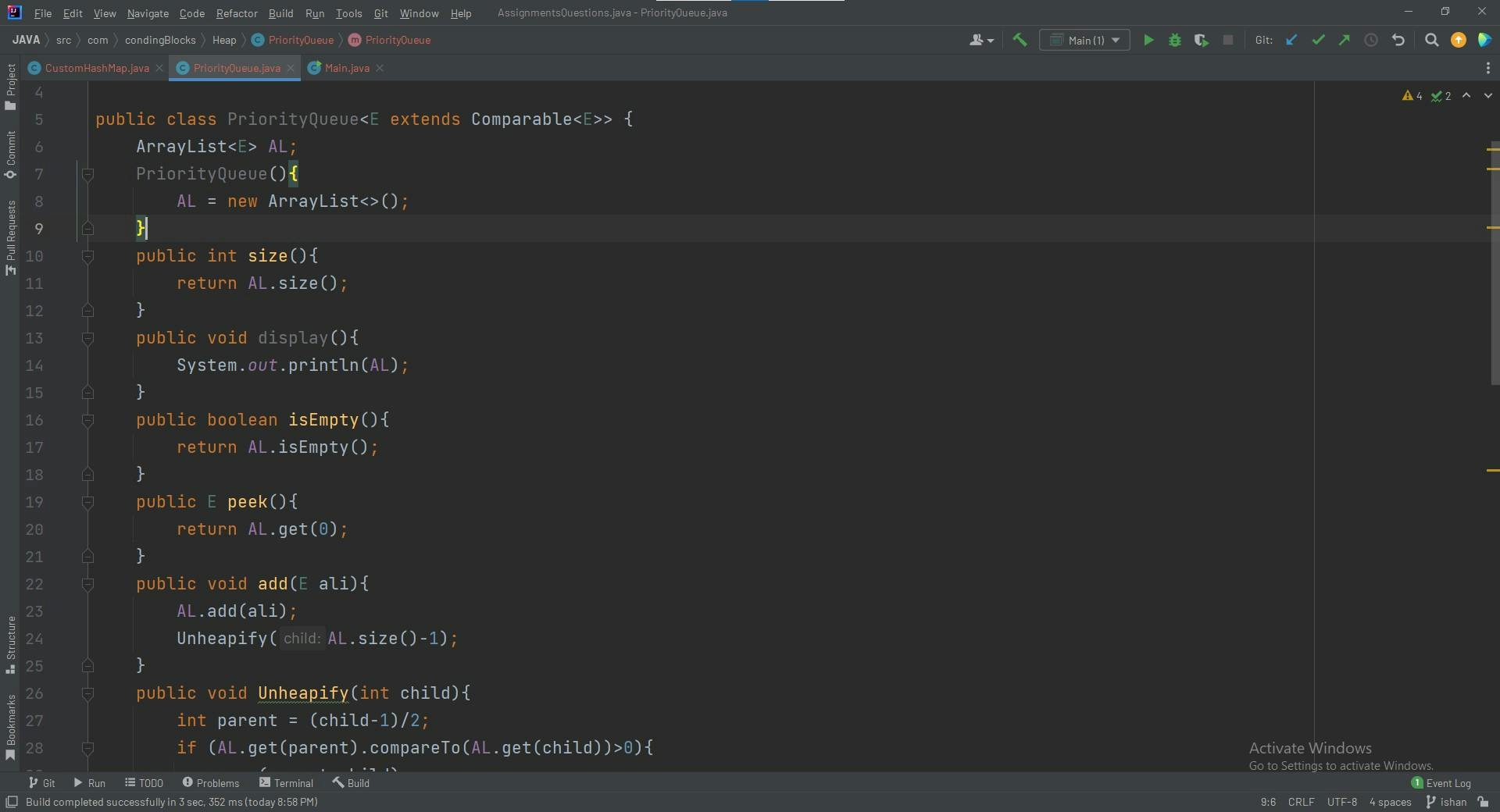
We are using ArrayList inside and as the priority queue is a generic data structure and we need to compare it in further functions so we are extending comparable.
Size, isEmpty, peek and display functions are pretty straightforward. Let's talk about the add function.
Add
So let me ask you a question, Where should I add the element in the ArrayList? Of course at the last index.
So if we add the element at the last and because we have to satisfy the condition of heap we need to check if the last element is greater than the parent or smaller as we are building a min-heap.
So checking the child with the parent and swapping it accordingly is called Heapify up.
So to heapify up we first need to get the parent index and the formula for that is - [child_Index-1/2]
In min-heap, if the child is greater than the parent after comparing it with the compareTo method. we are swapping it accordingly.
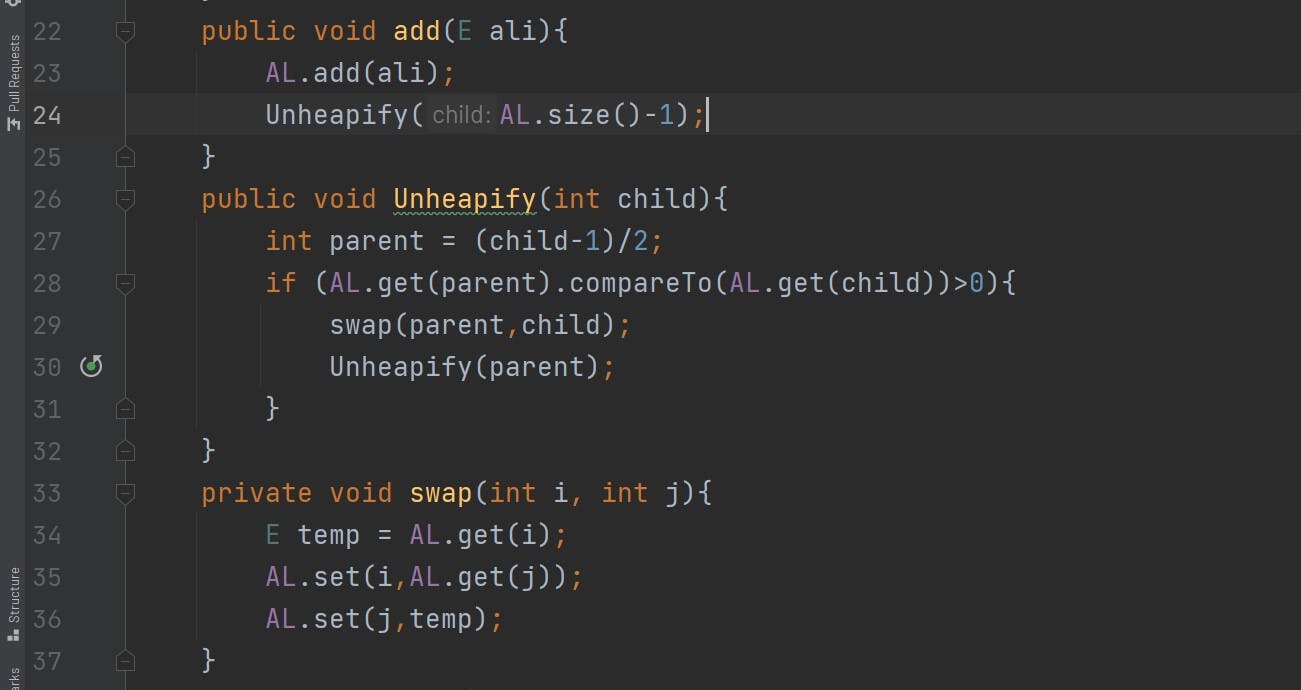
Forgive the typo but hope you got my point. Similarly, removing works
Remove
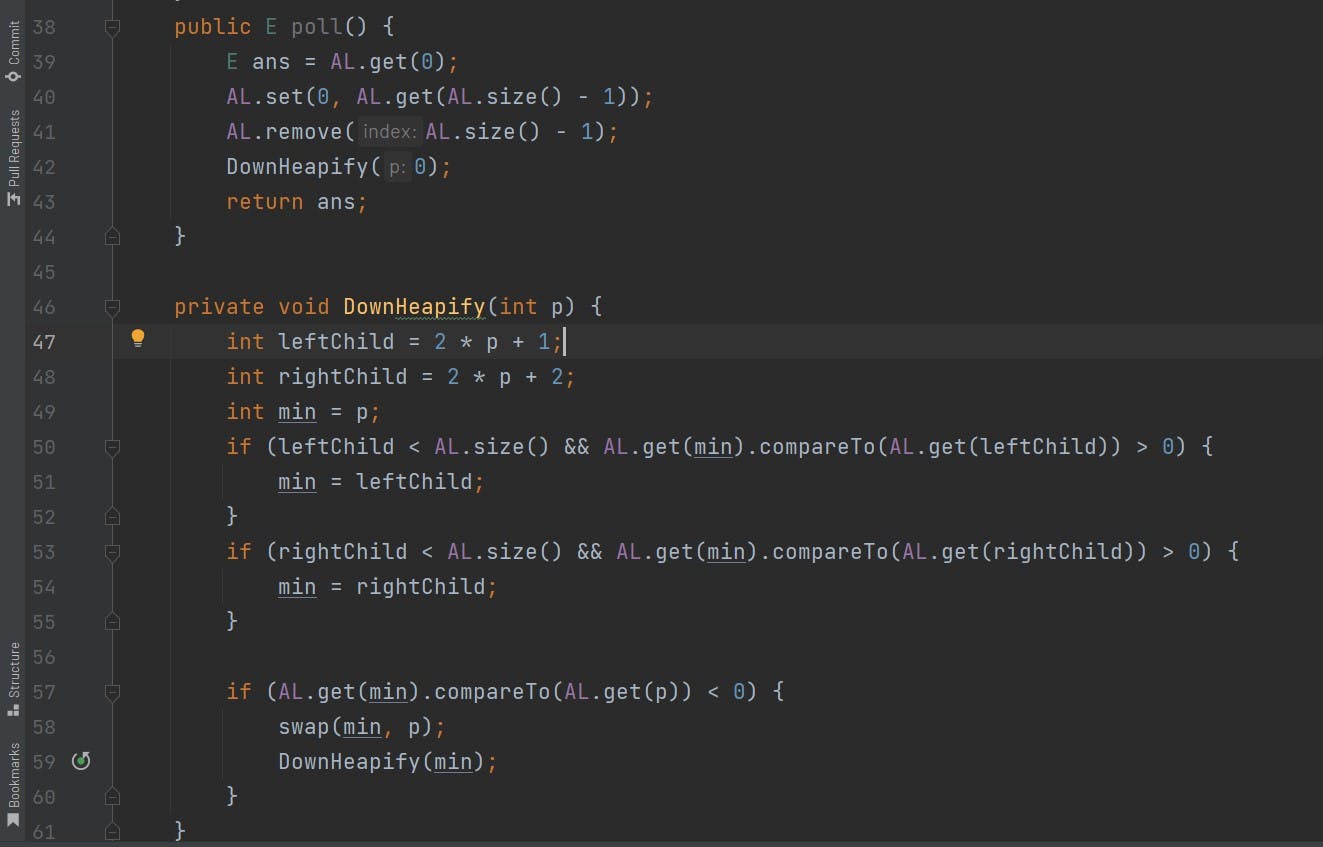
So another question, tell me which element will be the smallest element in the min-heap? Obviously, the root node because its a min-heap.
So while removing which element are we gonna remove obviously the root node, if we remove the root node then which node should come at the root node?
Now that is an interesting thing. If you see when you remove the root node the left subtree and the right subtree are a heap already so we do not want to touch that.
So to make it a heap which element should be added at the root node? Picking the root of the left subtree can disturb the heap and the same goes for the right subtree so to resolve that we gonna add the last node of the tree to the root node.
And by this, we will be adding the larger node to the root and it will disrupt the min-heap property so then we will use down heapify to make it a heap.
Down Heapify code is pretty straightforward. You just need to take the index of the left subtree parent and right subtree parent and compare it with the root node which you just added.
Sum Up
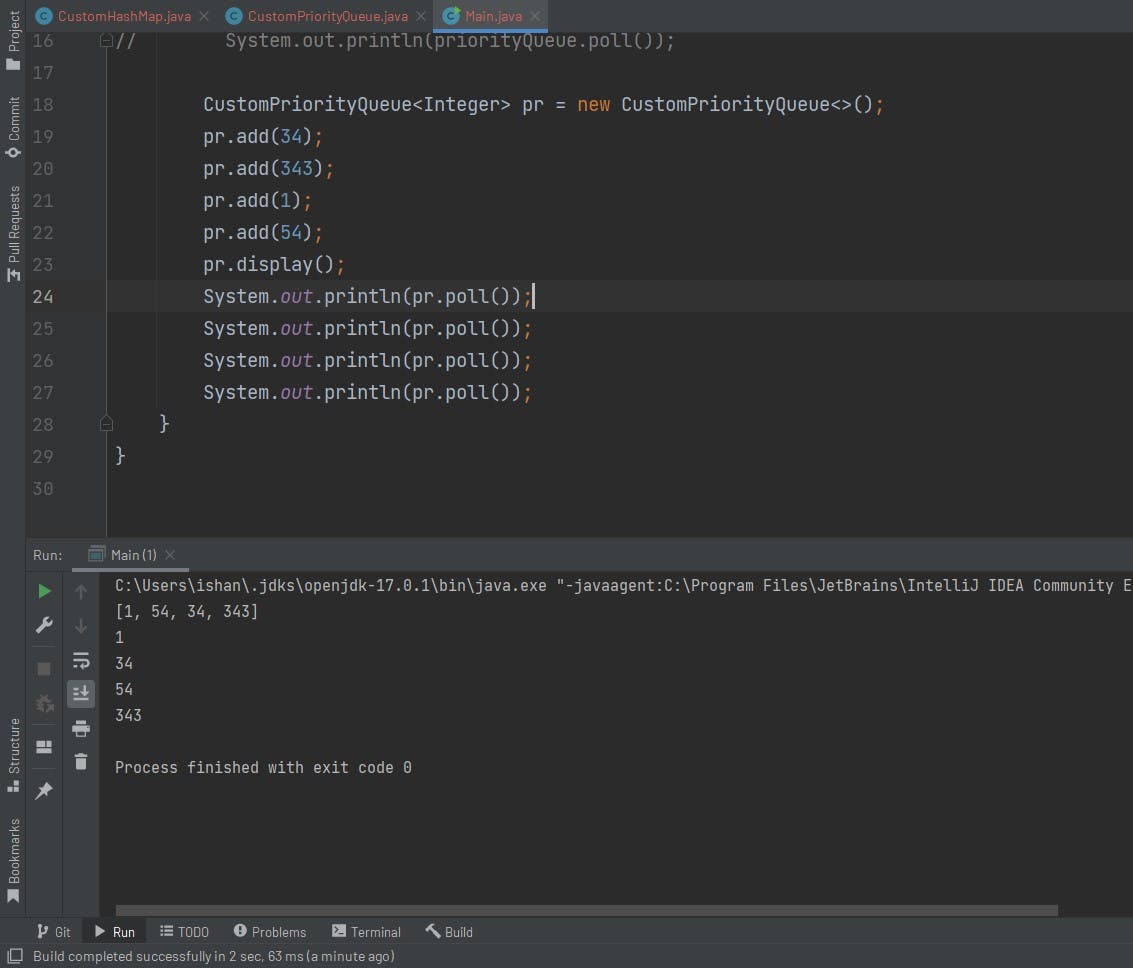
This is what the custom implementation of heap looks like and if you check the output it is exactly similar to the output of the java inbuilt priority queue was giving.
If you liked this article please subscribe to the newsletter and you can follow me on different social media accounts. I am open to feedbacks.

